用牛顿迭代法做开方运算-Java

一秉

在Java中，我们可以调用Math.sqrt()方法求解一个数的开方，我们将用牛顿迭代法 去求解一个数的开方。

首先随便猜一个近似值x，然后不断令x等于x和a/x的平均数，迭代个六七次后 x 的值就已经相当精确了。
例如，我们要求 根号2 等于多少。假如我猜测的结果为 1.6，虽然预测值不准，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号 2 了：

( 1.6 + 2/ 1.6 ) / 2 = 1.425
( 1.425 + 2/ 1.425 ) / 2 = 1.4142543..




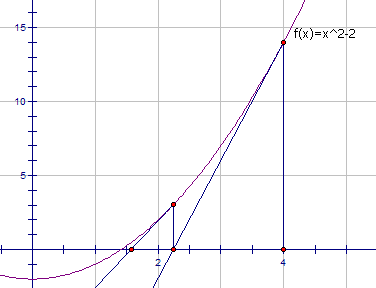
这种算法的原理很简单，就是不断用 (x,f(x)的切线来逼近方程 x^2−a=0的根。根号 a 实际上就是 x^2−a=0的一个正实根。f(x)的导数是 2x。也就是说，函数上任一点 (x,f(x)) 处的切线斜率是 2x。那么，x−f(x)/(2x) 就是一个比 x 更接近的近似值。
代入 f(x)=x^2−a得到 x−(x^2−a)/(2x)，也就是 (x+a/x)/2。

class Math {
       int s;
       public double sqrt(int x) {
             this.s=x;
             if(x==0) return 0;
                  return count(x);
             }

       }

       public double count(double x){
              double res = (x + s / x) / 2;
              if (Math.abs(res - x) < 0.0000001) {//当两个值相差的精度达到阈值时，结束代码
                  return x;
              } else {
                  return count(res);
              }
       }
}

代码如上所示。