|
红黑树是面试中一个很经典也很有难度的知识点,网传字节跳动面试官最喜欢问这个问题。很多人会觉得这个知识点太难,不想花太多功夫去了解,也有人会认为这个数据结构在日常开发中使用的很少,因此没必要多做掌握。 在此我针对以上两个观点做出一些纠正:首先,红黑树这个数据结构确实复杂,但是还没有到完全无法理解的地步。网上大多博客都不能够清晰完整的描述出红黑树的整个体系,对于红黑平衡调整的细节部分也没有很详尽的介绍,因此给学习带来了较大的困难。 其次,诸如Java中HashMap的底层实现,在JDK1.8中为了解决过度哈希冲突带来的长链表,会将链表转为红黑树;Linux底层的CFS进程调度算法中,vruntime利用红黑树来进行存储;多路复用技术的Epoll的核心结构也是红黑树+双向链表。 我们不会直接去手写一个可用的红黑树,但是了解红黑树的结构,有助于我们去理解一些底层具体实现。与此同时,红黑树也是对树结构的一种高度综合运用,涉及到多叉树,树平衡调整,节点旋转等等,这些是对数据结构基本功的最佳历练。 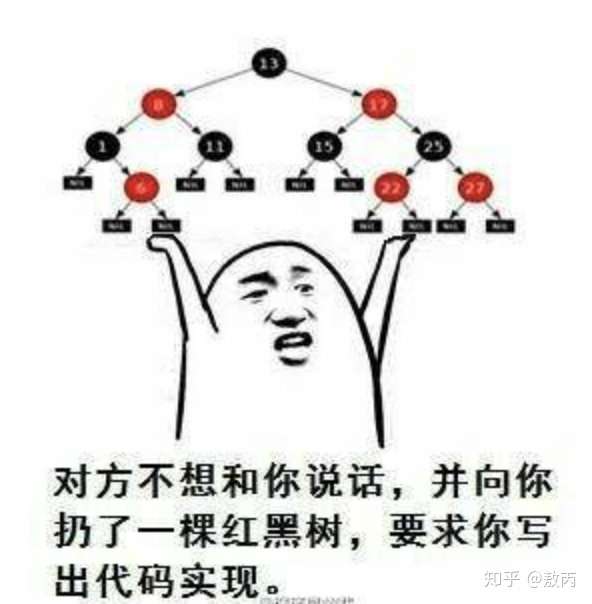 其实当面试官提出这个问题的时候,不参照答案,他大概率也无法清晰的给出具体的定义和操作。但是他希望从这个问题出发,看到你对于一个数据结构的理解,考察你知识面的广度和深度。能否给出完整的定义,能否介绍自己对红黑树的认识,能否通过旋转,染色等操作在给定的场景下对一颗红黑树进行调整使其符合定义......这些才是面试官希望从你的答案中得到的信息,问了一圈身边大厂的面试官朋友,跟我这个说法出入不大。 读完这篇文章,你将能够从红黑树的概念模型2-3-4树出发,理解红黑树五大定义背后的逻辑。你也可以深刻认识到红黑节点颜色背后的意义,对于插入删除引发的动态变化有一定的认识,而不再是去硬性的记忆某个场景下的调平操作(诸如:删除某节点,当该节点的叔父节点为红,而叔父节点的左右子节点都为黑的情况下,我们应该......)。你能够掌握节点旋转的具体操作,理解染色的目的。 最后,如果你足够认真,配图中有清晰的插入删除全部步骤,你能够真正的将红黑树变成自己的知识。 先谈平衡树做开发的朋友一定知道接口这个东西:定义接口,给出实现。一个接口可以有多种不同的实现,但是这些实现都会满足接口中的声明。 例如,我们定义手机是一个可用作通讯的工具,作为它的实现,三星,苹果,华为推出了各式各样的产品。 红黑树的本质其实也是对概念模型:2-3-4树的一种实现,因此我们先来关注2-3-4树。 2-3-4树是阶数为4的B树,B树,全名BalanceTree,平衡树。这种结构主要用来做查找。 关于B树(平衡多路查找树)的定义,网上已经有很多介绍,在此不多赘述。它最重要的特性在于平衡,这使得我们能够在最坏情况下也保持O(LogN)的时间复杂度实现查找(一个不具备平衡性的查找树可能退化成单链表,时间复杂度会到O(N))。 “ 在此需要提醒大家一下,平衡的定义是说从空链接到根节点距离相等,此处一定要用心理解。(也就是说非叶子节点是不会存在空链接的)
由于2-3-4树是一颗阶数为4的B树,所以它会存在以下节点: 2节点中存放着一个key[X],两个指针,分别指向小于X的子节点和大于X的子节点;3节点中存放在两个key[X,Y],三个指针,分别指向小于X的子节点,介于X~Y之间的子节点和大于Y的子节点;4节点可依此类推。 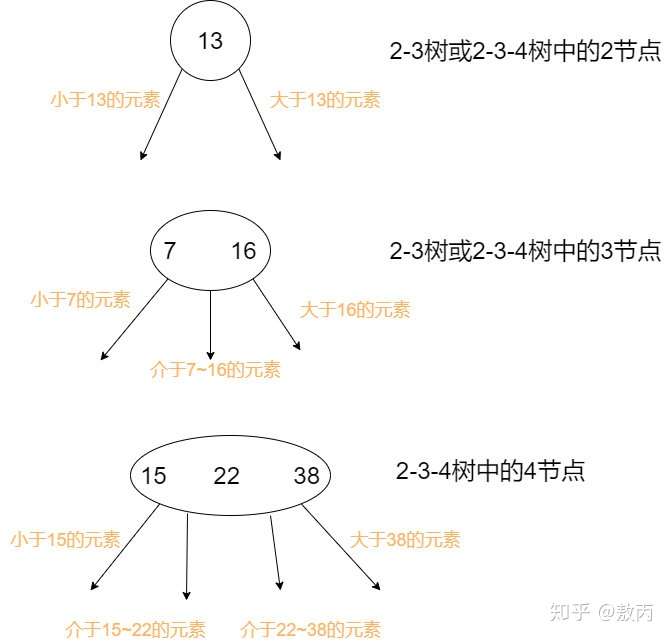 2-3-4树到红黑树的转化 2-3-4树到红黑树的转化红黑树是对概念模型2-3-4树的一种实现,由于直接进行不同节点间的转化会造成较大的开销,所以选择以二叉树为基础,在二叉树的属性中加入一个颜色属性来表示2-3-4树中不同的节点。 2-3-4树中的2节点对应着红黑树中的黑色节点,而2-3-4树中的非2节点是以红节点+黑节点的方式存在,红节点的意义是与黑色父节点结合,表达着2-3-4树中的3,4节点。 (此处理解成红节点也好,红色链接也好,看个人喜好。很多书中会说是由黑色节点指出的红色链接,链接指向的节点颜色为红。) 我们先看2-3-4树到红黑树的节点转换。2节点直接转化为黑色节点;3节点这里可以有两种表现形式,左倾红节点或者右倾红节点。而4节点被强制要求转化为一个黑父带着左右两个红色儿子。 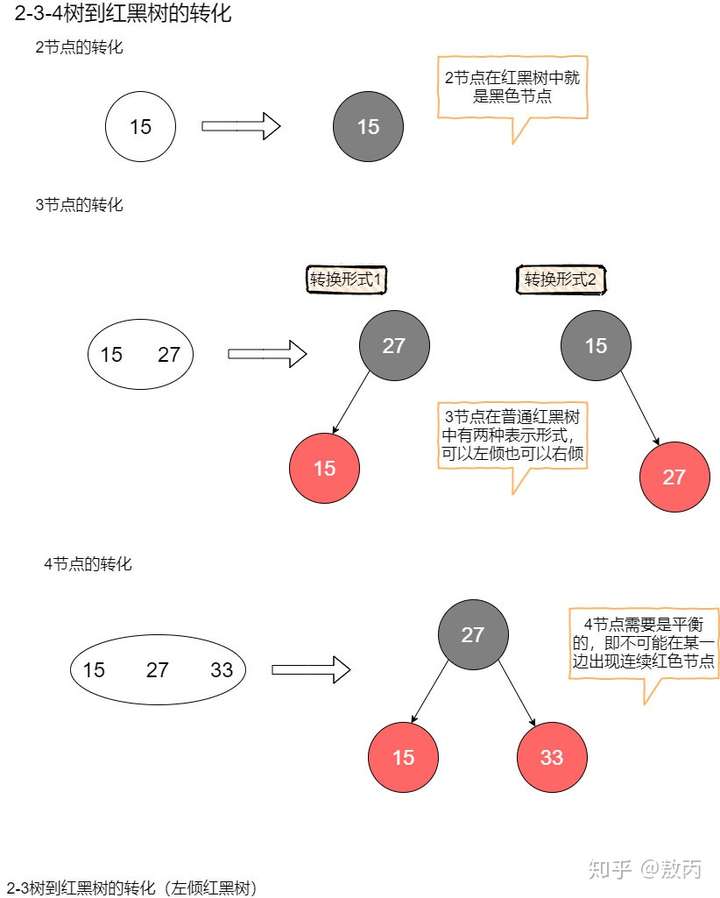
本文的研究主体是2-3树(原因会在后文给出),并且是2-3树中较为特殊的一种转化--左倾红黑树。顾名思义,左倾红黑树限制了如果在树中出现了红色节点,那么这个节点必须是左儿子。 以下是它的转化过程: 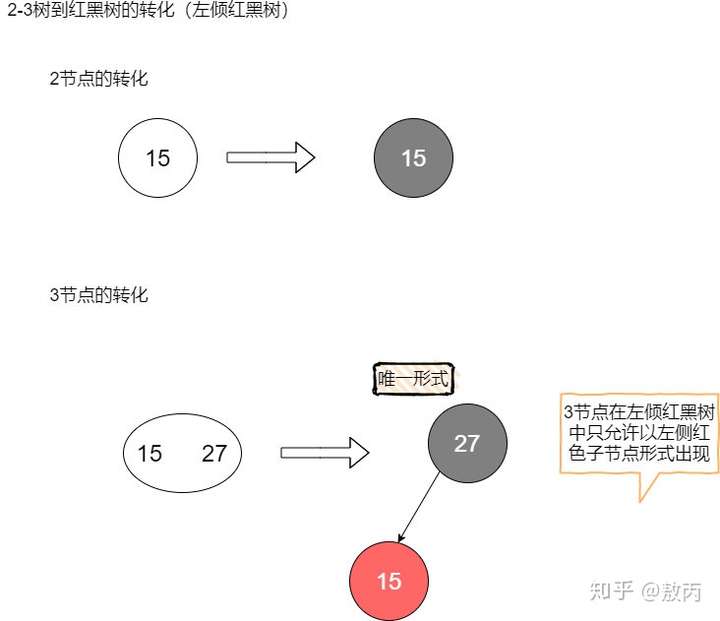 光看单个节点的转化可能还不够明显,我制作了一张红黑树转2-3树的示意图,很清晰地描绘了它们之间的关系。 只要把左倾红黑树中的红色节点顺时针方向旋转45°使其与黑父平行,然后再将它们看作一个整体,你就会发现,这不就是一颗2-3树吗? 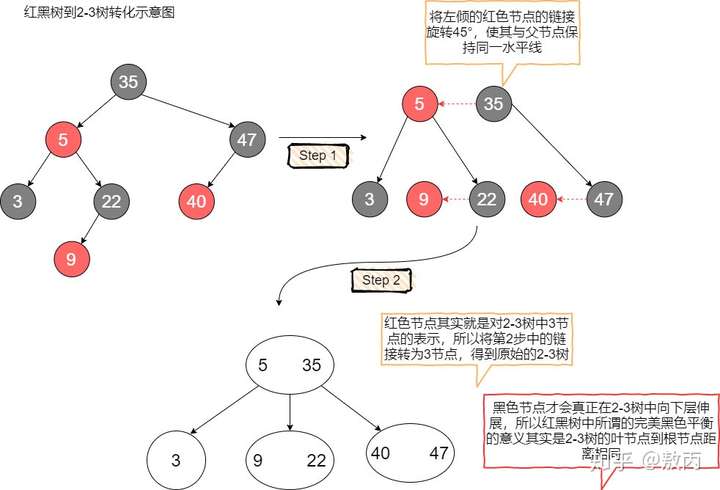 至此,我想大家已经明白,红黑树其实就是对概念模型2-3树(或者2-3-4树)的一种实现。 算法导论中给出的是红黑树基于2-3-4树实现,其中4节点要求平衡(即4节点必须用黑色父亲和左右两个红色儿子表示,红色儿子不能出现在同一边)。 算法4中给出的红黑树是基于2-3树实现,而且这种实现的红黑树十分特殊,它要求概念模型中的3节点在红黑树中必须用左倾的红色节点来表示。这种限定能够很大的减少红黑树调整过程中的复杂性,我们将在接下来的内容中体会到这一点。 我将算法导论和算法4中的红黑树反复的看了几遍,最终选择算法4中的红黑树做演示主体。 - 首先,算法4中的红黑树基于2-3树概念模型,不用考虑2-3-4树中复杂的4节点分裂;
- 第二,算法4中的红黑树是左倾红黑树,进一步降低了调平的难度;
- 第三,算法导论中对于红黑树删除场景的阐述并不够具体,许多关键环节都用“经过一定的旋转和变色处理”来带过,不利于新手的学习。(我花了很长时间还原具体过程)。
考虑到部分读者有充足的精力研究以2-3-4树为概念模型的红黑树,在介绍2-3树的同时也会带上2-3-4树的基础知识,帮助学有余力的读者去理解算法导论中的红黑树。(所以如果没有必要,只看2-3树的部分就行)。
我们在了解红黑树的插入删除操作之前,需要先了解2-3树的插入删除操作,这样才能理解红黑树中染色和旋转背后的意义。 让我们来看一下对于2-3树的插入。我们的插入操作需要遵循一个原则:先将这个元素尝试性地放在已经存在的节点中,如果要存放的节点是2节点,那么插入后会变成3节点,如果要存放的节点是3节点,那么插入后会变成4节点(临时)。然后,我们对可能生成的临时4节点进行分裂处理,使得临时4节点消失。
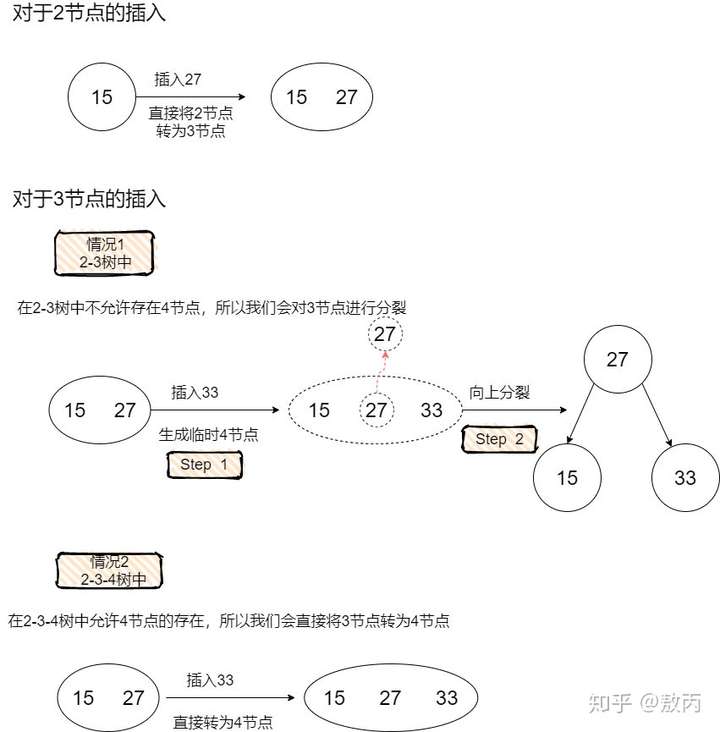 如果需要在2-3-4树中向4节点内插入元素,那么会引发如下图所示的分裂过程 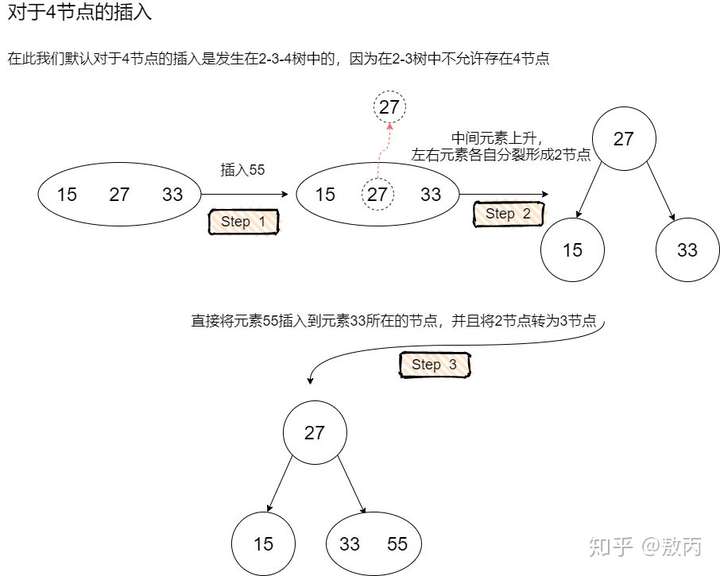 事实上,这正对应了红黑树在插入的时候一定会把待插入节点涂成红色,因为红色节点的意义是与父节点进行关联,形成概念模型2-3树中的3节点或者临时4节点。 而红黑树之所以需要在插入后进行调整,正是因为可能存在着概念模型中的临时4节点(反应在红黑树中是双红的情况)。 试想在2-3树中如果待插入节点是个2节点,那么反应在红黑树中,不正好对应着黑色父节点吗,在黑色父节点下面增加一个红色儿子,确实不会违背红黑树的任何规则,这也对应着我们向2-3树中的2节点插入一个元素,只需要简单的把2节点变成3节点。 接下来让我们来看一下对于2-3树的删除。对于2-3树的删除我们主要要考虑待删除元素在2节点这种情况,因为如果待删除元素在3节点,那么可以直接将这个元素删除,而不会破坏2-3树的任何性质(删除这个元素不会引起高度的变化)。 当待删除元素在2节点的时候,由于删除这个元素会导致2节点失去自己唯一的元素,引发2节点自身的删除,会使得树中某条路径的高度发生变化,树变得不平衡。 因此我们有两种方案去解决这个问题: - 第一种方案,先删除这个2节点,然后对树进行平衡调整。
- 第二种方案,我们想办法让这个被删除的元素不可能出现在2节点中。
本文选择第二种方案,我们在搜索到这个节点的路径中,不断地判断当前节点是否为2节点,如果是,就从它的兄弟节点或者它的父节点借一个元素,使得当前节点由2节点成为一个3节点或者一个临时4节点(视具体情况而定,在后面的红黑树部分会详细介绍)。 这种操作会产生一种结果:除非当前节点是根节点,否则当前节点的父节点一定是一个非2节点(因为搜索的路径是自上而下,父节点已经进行过了这种操作,所以不可能是2节点),那么我们可以保证到达叶子节点的时候,也能顺利的从父节点或者兄弟节点处借到元素,使得自己成为非2节点。从而能够直接删除某个元素(现在这个元素不在2节点中了)。 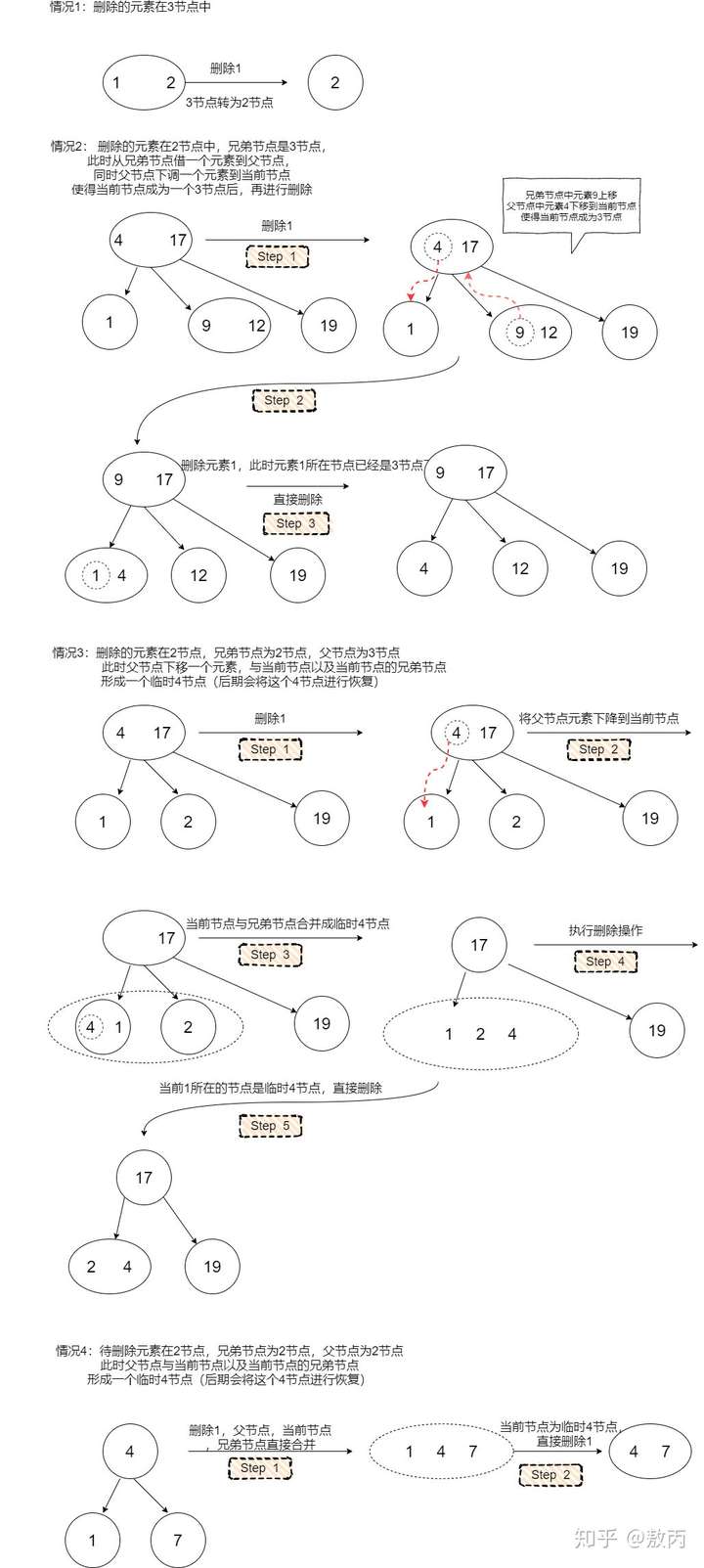
| 